(Solved) : Ingress Egress Nodes Suppose Given Acyclic Directed Graph G Represents Combinational Circu Q37352254 . . .
Ingress and Egress Nodes
Suppose you are given an acyclic directed graph G thatrepresents a combinational circuit C, where each node issub-circuit (e.g., AND gate, OR gate, NOT gate, 2:1 multiplexer,4:1 demultiplexer, 4-bit adder, etc) and directed edges are wires.Each node and edge has a nonnegative weight value that representsthe propagation delay of the circuit or wire. The propagation delayfor a node v is denoted by w(v), and the propagation delay for anedge (wire) connecting the output of circuit u to the input ofcircuit v is denoted by w(u,v).
Note that circuit C will have inputs and outputs. As shown inthe figure below, the inputs are at sub-circuits we will refer toas ingress sub-circuits, and the outputs are atsub-circuits we will refer to as egress sub-circuits.Similarly, nodes in G that correspond to ingress sub-circuits willbe referred to as ingress nodes, and node that correspond to egresssub-circuits will be referred to as egress nodes.
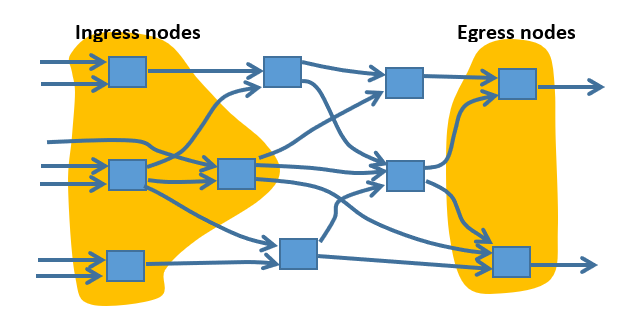
We will add new nodes s and t to G. Then add directed edges fromnode s to each ingress node, and node t has directed edges fromeach egress node. These new nodes and edges have zero propagationdelay.
We define the weight of a path from s to t to be the sum of theweights (propagation delays) of the vertices and edges along thepath. Note that the maximum weighted path is the criticalpath of the circuit, i.e., the path that dictates the overallpropagation delay of the circuit.
Describe an O(E + V) time algorithm that solves thisproblem. (Hint: Use Dag-Shortest-Paths Apply thealgorithm to the graph but with appropriate weights for thedirected edges.)
Ingress nodes Egress nodes Show transcribed image text
Expert Answer
Answer to Ingress Egress Nodes Suppose Given Acyclic Directed Graph G Represents Combinational Circu Q37352254 . . .
OR