(Solved) : Exercise 2 2 Pts Directed Graph Strongly Connected Pair Vertices U Y Path U V Path V U Con Q44082117 . . .
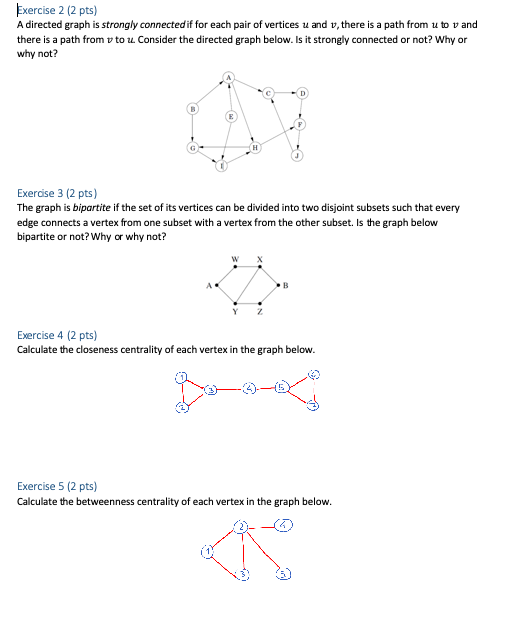
Exercise 2 (2 pts) A directed graph is strongly connected if for each pair of vertices u and y, there is a path from u to v and there is a path from v to u. Consider the directed graph below. Is it strongly connected or not? Why or why not? Exercise 3 (2 pts) The graph is bipartite if the set of its vertices can be divided into two disjoint subsets such that every edge connects a vertex from one subset with a vertex from the other subset. Is the graph below bipartite or not? Why or why not? Exercise 4 (2 pts) Calculate the closeness centrality of each vertex in the graph below. Exercise 5 (2 pts) Calculate the betweenness centrality of each vertex in the graph below. Show transcribed image text Exercise 2 (2 pts) A directed graph is strongly connected if for each pair of vertices u and y, there is a path from u to v and there is a path from v to u. Consider the directed graph below. Is it strongly connected or not? Why or why not? Exercise 3 (2 pts) The graph is bipartite if the set of its vertices can be divided into two disjoint subsets such that every edge connects a vertex from one subset with a vertex from the other subset. Is the graph below bipartite or not? Why or why not? Exercise 4 (2 pts) Calculate the closeness centrality of each vertex in the graph below. Exercise 5 (2 pts) Calculate the betweenness centrality of each vertex in the graph below.
Expert Answer
Answer to Exercise 2 (2 pts) A directed graph is strongly connected if for each pair of vertices u and y, there is a path from u t…
OR